In my
2021 Bridges paper,
and also at the 2020 cfc origami creators event, I talked about families of deformations of the waterbomb base
tessellation, and also about how or whether it might be possible to combine two one parameter
families of deformations to create one two parameter family.
This page gives an example of another situation of combining two parameters, which I didn't
cover in my talk.
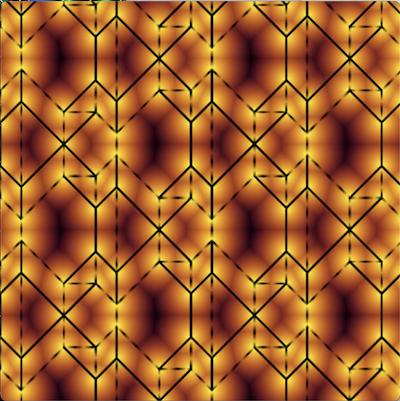
The first family on this page is the two peak waterbomb variation,
which is on my
multipeak waterbomb base tessellation page, and is obtained with b=c=0.
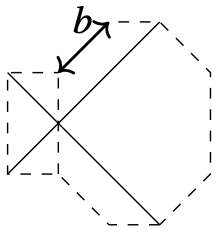
The other family is the dragon scales variation, which is one of the families on
my page
combining LamiOri and dragon scales tessellations.
If you want a challenge, before looking at the program below,
look at the following two pictures, and try and work out
how to combine them into one family with two parameters.
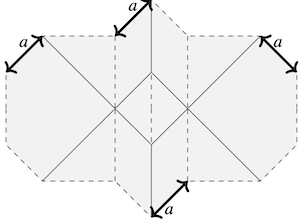
That is, given a family with a as a parameter, and another family with b as
a parameter, as shown in these diagrams, is there a family with
two parameters, which restricts to these two families
when one parameter
is zero? Or, if not zero, if we restrict to some
one dimensional subspace of the 2-dimensional parameter space.
To make this question non trivial, we require that there
are sides of the parameterised unit which have lengths a and b.
A possible solution is given below.
In this solution, the lengths do not change direction, though I do not know
if this should be a requirement for a solution, or if other solutions without
this condition exist, or other solutions with this condition.
My question is still not completely precisely defined.... I have an answer looking for the right question.


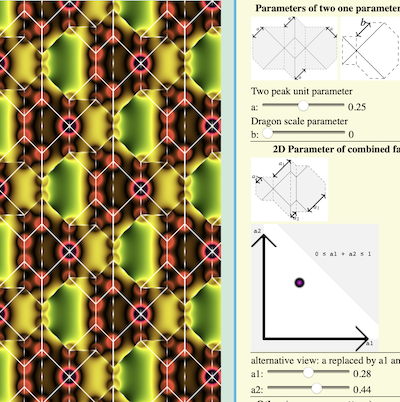
| Parameters of two one parameter families: |
|---|


|
| Two peak unit parameter |
| a: 0 |
|
Dragon scale parameter
b: 0 |
| 2D Parameter of combined family: |
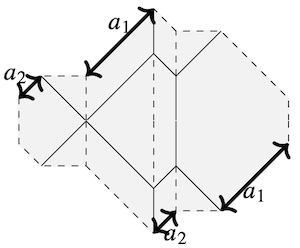
|
|
a1
a2
0 ≤ a1 + a2 ≤ 1
|
|
alternative view:
a replaced by a1 and a2
a1: 0 |
| a2: 0 |
| Other (non crease pattern) parameters for image |
| scale: 1 |
| shift x-coord: 0 |
| shift y-coord: 0 |
| line width: 1 |
|
Colour variables:
var 1: 0 |
| var 2: 0 |
| var 3: 0.5 |
| var 4: 0 |
One way to think of this variation is that the value of a in
the labeled figure is replaced by two variables, a1 and a2.
I would guess that applying the same method to the multipeak unit would replace b by b1, b2 and
c by c1, c2, in a similar way to how a is replaced by a1, a2,
giving a 6 parameter family. The dragon scales parameter may be thought of as changing a1, while
keeping a2=0.
Maybe this family could be thought of as resulting when we try to apply the dragon scales
families on both left and right sides of the unit, so the "spreading out" of this family could
go in either direction.
The total height of the unit (molecule) in the tessellation
is fixed at 1 unit, and the width is
1 + 2a1 + 2a2.
There is a limit, a1 + a2<=1,
so the max possible values of a1 and a2 are changed as they change.
I have made a and b sliders only possible to be non zero one at a time, to
be able to illustrate these two one dimensional families separately.
The values can both be made nonzero with the other sliders.
Whereas for the combination of the LamiOri and dragon scales tessellations, the original families are found in the axes of the two parameter family, in this case, the dragon scales family is the a1 axis (the axis with a2=0), the two peak unit family is the diagonal subspace with a1=a2.
Note, although in my program I have fixed the unit height at 1 (or more precisely, I have fixed the distance between the center line of one row and the center line of the next row to be 1), in the labeled figures, the length of the lefthand and right hand ends of the unit are fixed (they do not have arrows on to indicate varying length, so it would be natural to assume constant length). As the parameters a1, a2 are changed, you will see that the end height of the unit changes. This inconsistancy between the images can be rectified by applying an overall scale factor, which would rescale the ends to one. There is an option to scale. I could rewrite the program at some point to automatically scale appropriately. I choose my average unit height to remain constant so that the rows stay in the same position, so the units move less as the the parameters vary.
The above program is tested in safari on a mac, and might not work in
other browsers. In case you are unable to use this program,
here are a couple of pictures of tessellations obtained from print outs
from this program. I have three models here, with picture of program output
and how it looks folded.
I could give these titles!
How about "purple peaks", "islands in the sea",
and "lava flow"? Last two pictures are a screenshot of the program, and
a picture of another crease pattern I have not folded yet.