Note on controls:
Most of the controls are for my own use for illustrating different concepts, but it's easier to have only one program rather than two.The preset examples show lots of examples, that you can adjust with the sliders and radio buttons. The different settings were used to try to make various different concepts clearer, and to experiment with the visual depiction. I included a lot of examples.
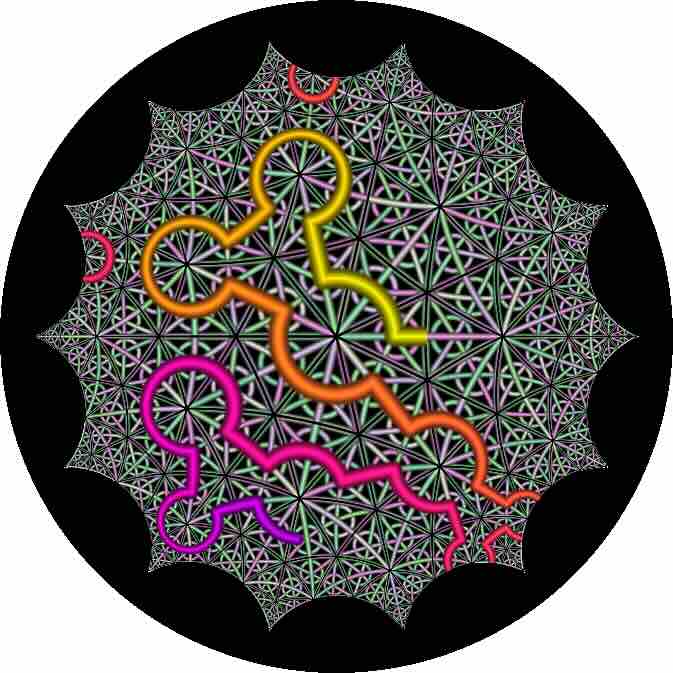
- "time" just controls the position of a point passing along the Hamiltonian cycle; "before" this point is coloured, "after" is black
- "time-frac" is for changing time fractional part, to make it easier to see the change. This starts at 0.5, because I wanted the picture to remain constant for a bit before changing, so if you start this at 0, the slider doesn't appear to be doing anything (on the fano plane picture) until 0.5 anyway.
- "generators" gives one of the possible choices of matching of the generators for the automorphism group of the Klein quartic with the generators of the automorphims of the Fano plane. What does this mean? Very briefly, you can see the correspondence (isomorphism) by noting that if two triangles in the tiling of the Klein quartic are related by a rotation of a particular order, then the arrangement of the lines (in the Fano arrangement) on these triangles are related by a permutation of the same order. Note that the generator choice 336 does not correspond to generators at all, just a list of all the elements of the automorphism group in a relatively nice combinatorial way, corresponding to choosing a position for three fixed non-colinear cards one by one. This corresponds to the original choice of ordering of arrangements in the program I wrote for a game based on "mini Dobble". Apart from 336, the choice of generators always gives a regular motion of the points on the rearangements of the cards, but only for the first 21 choices of generator pairs will we get generators that visually correspond to triangles that match up along edges in the placement on the Klein quartic tiling. This is explained in the link to the paper and talk.
- "widthH" is the width of the black Hamiltonian path line
- "widthHC" is the width of the colour part of Hamiltonian path line
- "widthHB" is the width of the black lines bordering hexagons
- "widthHB2" is the width of the white lines bordering hexagons
- "widthB1" and "widthB2" are for the boundary of the triangles
- Colour option: (1) is my first choice of bright colours; (2), (3), (4) are an attempt to give a choice for people who might be colour blind. (5) shows one choice black, the others pale, so the movement of the black line can be more easily picked out. (6) is a random choice; you'll get different values each time you choose this. (7) is a choice to be used with disc pattern (2), where discs are solid colours, and red, blue, green are a basis, so we can see how the other discs on a line are determined by the sum of the colours, e.g., on the line with red, blue discs, the third disc is magenta, since red+blue = magenta (light addition).
- Disc patterns (1) each disc is on three lines; the dots on the discs correspond to the colours of these three lines. (2) is a dual version, where the line colours are determined by the disc colours. (3) is a version where the discs have a larger border to more easily track their movement (note, one of the radius sliders can change the disc size). (4) Colour is average of line colours disc lies on.
- Disc numbers: Various configurations; maybe it's interesting to see the path of just one disc. Maybe it's interesting to see how x number move and interact. Maybe it's interesting to look at how colinearity or non colinearity is preserved; maybe basis or projective frame of reference is interesting. So various options.
- WidthF1: widths of Fano triangle lines (in Klein quartic arrangement)
- WidthF1: widths of other Fano triangle lines (in Klein quartic arrangement)
- ShadeF1: brightness of Fano lines (in Klein quartic arrangement)
- ShadeF2: sharpness of edges of Fano lines (in Klein quartic arrangement)
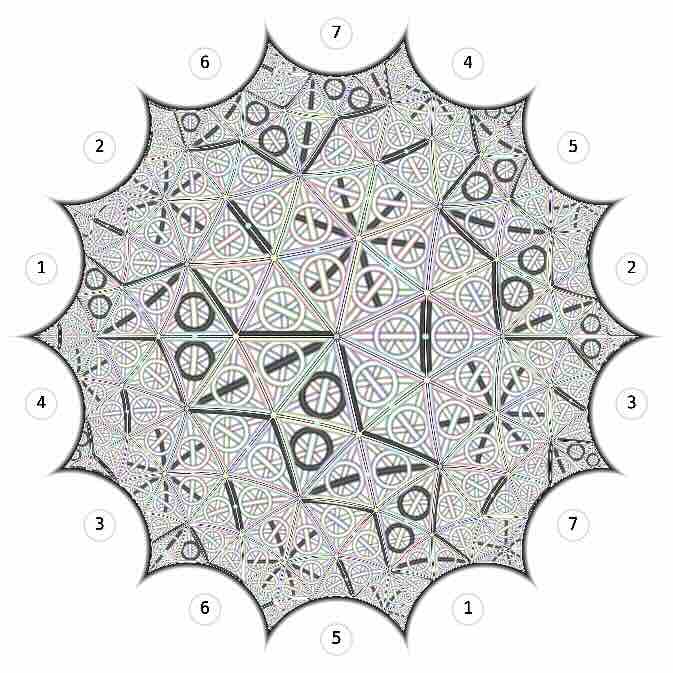
- Euclidean or hyperbolic shows the Fano planes either arranged on the Klein quartic, which is what this program is all about, or else alternatively, just laid out in a grid, which looses all the structure of the relationships between the arrangements, but is available for considering the limitations of this format
- labels on/off is to show or not show the edge identifications of the Klein quartic
- Originally, I made the points (mini Dobble cards) move, and the lines just changed colour. Then I thought about having the lines transform. The points just move linearly from start to end positions between each configuration. This is not a great choice for determining movement of lines; I put in different options for line transformation; neither great; ideally would have something corresponding to the corresponding element of PGL(3,2), but since the plane is not mod 2, this might not be possible. (PGL(3,2): 3x3 matrices with entries 0 or 1). Unfortunately the animations for these are pretty bad, but not had time to fix yet.
- I put in the option to put in some small corner pictures, to illustrate some of the concepts, in a printed out version
- I will try and get round to adding more notes at some point
The Fano plane
The Fano plane is a collection of 7 points and 7 lines. Each line has three points on it, each point is on three lines, every two lines intersect at some point, every two points are on a common line.The automorphisms
An automorphism of the Fano plane is a way of switching round the points in such a way that if points were on a common line before switching, they are still on a common line after switching, etc; all the relationships are the same after switching as before. There are 168 such automorphisms. I've put these into a game here. There are lots of websites dicussing the Fano plane and its automorphisms. E.g. Wikipedia.
An article by Shintaro Fushida-Hardy describing a crochet Klein quartic and automorphisms of the Fano plane can be found here (same article here.
The Cayley graph
A graph can be drawn of the elements of the automorphism group. This is graph in the sense of vertices (points), joined by edges: Draw a dot for each element of the automorphism group; Choose some generators, and connect the dots by directed arrows if they are related by multiplication by one of the chosen generators. For more details, see Wikipedia and group theory and finite geometry textbooks and web pages, etc, e.g., Group Properties Wik.Choose different generators, and you'll get a different graph. There is a nice example at Webb.
Every element of the automorphism group is listed on this wikiversity page.
I've taken two generators, one of order 2, and the other of order 7. I've chosen 21 different possible pairs of generators. you can change these with the given slider.
Now use the fact that the automorphism groups of the Fano plane and the Klein quartic are isomorphic. See the Wikipedia page on the Klein quartic. This program illustrates an example of an isomorphism between the automorpshim groups. For the Klein quartic, each automorphism is uniquely determined by the image of a chosen triangle, so the triangles in the Klein quartic picture correspond to elements of the automorphism group, so give an easy way to draw a Cayley graph.
I want to step through the elements of the automorphism group in a nice way. Nice is subjective; for me, for this work, nice means working my way through a Hamiltonian cycle on a Cayley graph.
Some example images (a reduced size/quality jpg version obtained from the png output):